Mọi người có bao giờ thắc mắc lý do vì sao mà hoa loa kèn lại có ba cách, trong khi đó bông cúc vạn thọ thì gồm 13 cánh, nhưng hoa cúc tây thì là 21 cánh. Hay hoa cúc lại đa dạng từ 34 cho đến 55 hay là 89 cánh hay không? Những sự xuất hiện đó còn được hiểu và áp dụng theo dạng dãy Fibonacci trong tự nhiên. Tại bài chia sẻ này sẽ cung cấp đầy đủ thông tin cho bạn đọc, theo dõi ngay nhé!
Khái niệm về dãy Fibonacci
Trước khi tìm hiểu dãy Fibonacci trong tự nhiên là gì thì chúng ta cần phải hiểu rõ về khái niệm của thuật ngữ dãy Fibonacci. Đây là một dãy số kinh điển ở trong lĩnh vực toán học, đã được tìm thấy từ thời điểm cách đây khoảng 800 năm. Đến hiện tại, nhiều nhà khoa học đã có sự phát hiện hay ho về dãy số này ở trong tự nhiên.
Dãy số này là một dãy số vô hạn bao gồm những số tự nhiên được khởi nguồn bởi 1 và 1, tiếp đến là những số tiếp theo sẽ tính bằng tổng của hai số liền kề trước chúng. Chi tiết, những số ban đầu của dãy số này là 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610.
Chi tiết dãy Fibonacci trong tự nhiên

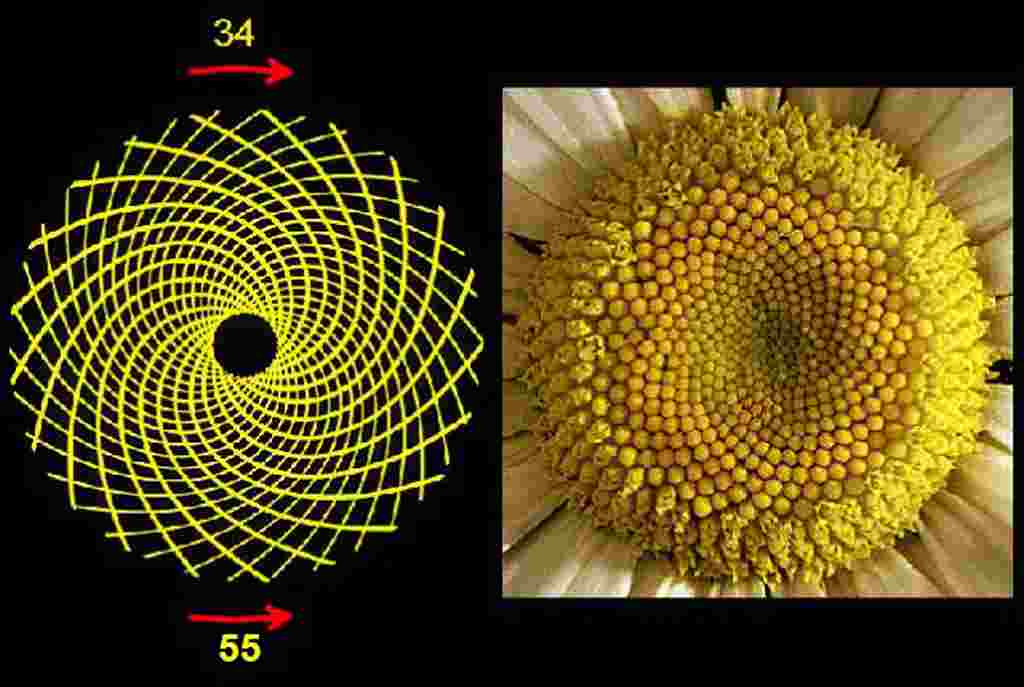
Ngày nay, trong tự nhiên xuất hiện nhiều sự trùng hợp đối với những dãy số này hay là các tỷ lệ vàng. Đa số những bông hoa đều có số cánh bao gồm các số như sau: 3, 5, 8,13, 21, 34, 55 hay là 89. Giả sử, bông loa kèn sẽ có 3 cánh, bông mao lương màu vàng thì có 5 cánh, bông cải ô rô lại sẽ có 8 cánh, bông hoa cúc vạn thọ bao gồm 13 cánh. Ngoài ra, bông cúc tây thì có 21 cánh, nhưng bông cúc dạng thông thường thì lại có 34 hay 55 hay là 89 cánh. Thật thú vị phải không?
Đối với bông hướng dương
Những dãy Fibonacci trong tự nhiên được áp dụng đối với cả bông hướng dương. Chi tiết tại bông hướng dương thì các nụ nhỏ sẽ được sắp xếp theo hai tập hợp bởi những đường dạng xoắn ốc. Trong đó một tập sẽ được cuốn theo chiều của kim đồng hồ, còn một tập sẽ ngược lại theo chiều còn lại của kim đồng hồ.
Đối với trái thơm
Nếu như mọi người quan sát những mắt nằm trên vỏ của những thái thơm thì dễ dàng nhìn thấy được các số mắt trên đó gồm hai đường theo dạng vòng cung chéo ngay tại vỏ trái dứa. Cụ thể là hai số của dãy Fibonacci trong tự nhiên như là 13 hoặc là 21.
Đối với số nhánh cây
Số nhánh của từng cây từ khi nó đi ở phía gốc lên phía trên ngọn thông thường cũng sẽ áp dụng theo dãy Fibonacci này. Từ một nhánh lên hai nhánh, từ ba nhánh rồi thành năm, tám hay là mười ba nhánh. Các lá ở một cành cây cũng sẽ được mọc cách nhau từng khoảng giống như là dãy số của Fibonacci này.
Ngoài ra hiện nay còn nhiều trường hợp khác áp dụng dãy Fibonacci, đồng thời có sự liên kết giữa tỷ lệ vàng cũng như dãy Fibonacci. Như là hình dạng của một vỏ ốc tương đương như là đường cong theo tỷ lệ vàng. Hay một hình ảnh khác là lỗ tai của con người đồng nhất với đường cong của tỷ lệ vàng. Bên cạnh đó, những cơn bão mà chúng ta thường thấy cũng được áp dụng theo, hay kể cả khuôn mặt của con người chúng ta cũng cân đối so với các tỷ lệ vàng.
Lý do vì sao lại có dãy Fibonacci trong tự nhiên?
Liệu các điều trùng hợp phía trên có phải là những trường hợp ngẫu nhiên hay không? Câu trả là là không. Mọi thứ đều thuộc dãy Fibonacci bao gồm những dãy số như ở phía trên chúng tôi đã nhắc tới. Thực tế là tất cả đều được tuân theo một quy luật, định luật chung. Cho dù mọi người có thể có câu trả lời, câu giải thích chi tiết hay là không.
Hay giống như tỷ lệ vàng, các tỷ lệ kỳ diệu của tạo hóa mang đến, Fibonacci trong tự nhiên này cũng là một trong những quy luật chung của mọi điều trong cuộc sống này. Và việc này liệu có công nhận theo giả thuyết là thế giới này đã được tạo ra dựa vào bàn tay của chúa, người đã nhào nặn mọi thứ theo các quy luật riêng hay không?
Với một thời gian rất dài, chúng ta vẫn không thể tìm được câu trả lời vì sao các con số kia lại có sự xuất hiện dựa theo quy luật như nhiên như thế. Chỉ với một vài năm gần đây thì chúng ta mới hiểu được, thực vật trong giai đoạn tiến hóa của chúng sẽ luôn có xu hướng thay đổi, hoàn thiển để có thể hòa hợp tốt nhất đối với môi trường sống của chúng. Ngoài ra, để có thể duy trì được mức tăng trưởng phù hợp thì giữa chúng sẽ có một mối liên quan nhất định.
Một số ví dụ điển hình về dãy Fibonacci trong tự nhiên

Bông hoa hướng dương
Hãy tưởng tượng rằng nhị của bông hoa hướng dương được tạo nên từ các hạt nhỏ. Đầu tiên tại trung tâm của chúng, tiếp đến di chuyển sang phía bên ngoài, sau cùng là khi mọi hạt đã được tạo nên thì chúng sẽ phải sắp xếp phù hợp với diện tích. Nhờ vậy mà có được nhiều loại hạt nhất, đồng thời giúp cho tỷ lệ thụ phấn mới đem lại kết quả tối ưu.
Giả sử bây giờ chúng tiến hành di chuyển dần dần từ phía trung tâm ra phía ngoại vi theo dạng nan hoa. Thì lúc này khoảng cách trống giữa những hàng lá tương đối nhiều, đặc biệt là ở phần ngoại vi của hoa. Vậy là đây không phải cách tối ưu nhất.
Để có thể tối ưu nhất về không gian thì những đường thẳng phía trên phải bắt buộc uốn cong theo dạng hướng. Nhưng việc cong một góc khoảng bao nhiêu độ thì phần diện tích về không gian sẽ có thể chiếm tối thiểu. Việc này là một điều vô cùng kỳ diệu của tạo hóa.
Các nhà khoa học đã chứng minh, với tỷ lệ vàng đã đóng góp vai trò vô cùng quan trọng đối với cách tính góc xoay trên. Về cơ bản, một đường từ phía tâm đi ra ngoại vi sẽ có thể xoay lên đến 360 độ. Người đọc có thể sử dụng một mẹo chia sẻ nhỏ là bằng góc xoay của bông hoa hướng dương ngay phần nhị.
Quá trình mọc của lá cây
Có đa dạng loại cây có hình thức mọc lá áp dụng và tuân thủ Fibonacci trong tự nhiên. Nếu như quan sát kỹ, chúng ta sẽ nhìn thấy những lá cây ở phía cao thông thường được sắp xếp làm sao mà không che khuất đi các phần lá mọc ở phía dưới. Việc này tức là từng lá sẽ được nhận mức nước hay ánh sáng phù hợp.
Nếu như từ phía mỗi lá ngọn làm phần khởi đầu, xoay quanh phần thân cây từ phía trên xuống phía dưới, từ lá này sang lá khác, sau đó đếm số vòng xoay và số lá, thì chúng ta sẽ nhận thấy dãy số này xuất hiện. Ngoài ra nếu như mọi người tiến hành đếm ngược thì sẽ xuất hiện một con số có vòng xoay riêng. Điều kỳ diệu là những con số tại vòng xoay theo hai hướng sẽ cùng với các số lá cây mà mọi người đã gặp khi tiến hành xoay. Mọi thứ sẽ được tạo nên ba dãy số này liên tiếp nhau.
Theo như chúng ta biết ở trong bài chia sẻ này từ đầu đến giờ, dãy Fibonacci trong tự nhiên là một điều vô cùng thú vị và diệu kỳ. Những quy luật mà không ai có thể giải thích được vẫn tồn tại ngày qua ngày theo thời gian. Mong rằng với những kiến thức và chia sẻ này sẽ hữu ích cho bạn đọc trong quá trình tìm hiểu, áp dụng trong cuộc sống hàng ngày nhé.