Phân tích hệ số tương quan là một trong số các giai đoạn quan trọng trong quá trình phân tích và làm việc ở mảng tài chính. Đây là một trong số các hệ số được ứng dụng rộng rãi kể cả ở mảng đầu tư. Bài viết sẽ cung cấp thông tin về hệ số tương quan là gì? Cách tính hệ số tương quan và ứng dụng trong các lĩnh vực tài chính, đầu tư.
1. Hệ số tương quan là gì?
Hệ số tương quan được xem là cách đo lường về mức độ mạnh yếu của sự tương quan giữa các biến động tương đối của 2 biến bất kỳ. Những biến có giá trị này từ âm 1 đến 1. Một vài trường hợp có thể lớn hơn 1 hay nhỏ hơn âm 1 thì phép tính đã xảy ra trục trặc khi đo lường. Mỗi tương quan âm 1 thể hiện sự liên kết âm tuyệt đối, còn ngược lại mối tương quan 1 thể hiện sự liên kết dương tuyệt đối. Còn nếu kết quả là 0 thì giữa 2 biến này khi biến động không có sự liên kết tuyến tính nào.
Có một vài dạng hệ số tương quan tuy nhiên dạng hệ số tương quan Pearson hay R là hệ số dùng phổ biến, R là thông số phản ánh mức độ mạnh và hướng của mỗi liên kết tuyến tính giữa 2 biến.
Nếu kết quả tính ra được là 1 thì hai biến này có một mối tương quan dương tuyệt đối, tức là khi mà một biến tăng lên biến kia cũng sẽ tăng theo tương tự. Nếu tính ra kết quả là âm 1 tức là hai biến có mối tương quan âm tuyệt đối, nếu biến này giảm biến kia sẽ tăng và trái lại.
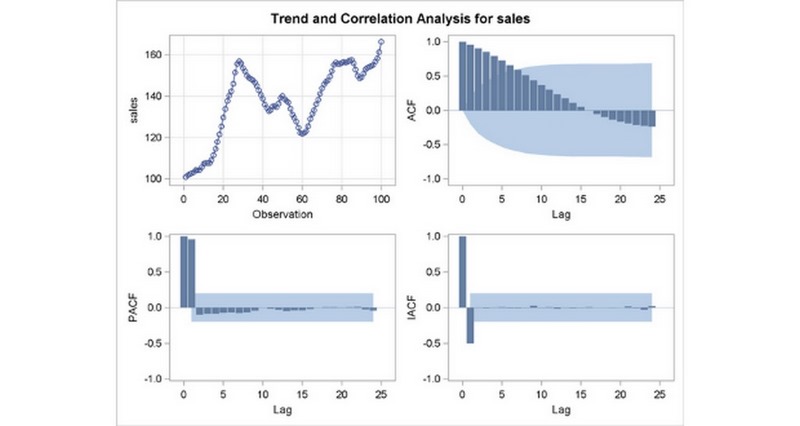
2. Cách tính hệ số tương quan như thế nào?
Như đã đề cập thì hệ số tương quan có khá đa dạng những loại riêng biệt tuy nhiên loại được dùng nhiều là hệ số tương quan R hay Pearson. Dạng tương quan này phản ánh được thông số tính toán những mối liên kết phi tuyến tính giữa 2 biến và không nhận ra được đâu là biến độc lập và phụ thuộc.
Cách tính hệ số tương quan được phản ánh qua cách tính sau:
Trong đó:
ρxy: Là hệ số tương quan Pearson.
Cov(x, y): hiệp phương sai với 2 biến x và y.
σx: độ lệch chuẩn của x.
σy: độ lệch chuẩn của y.
Độ lệch chuẩn là thông số phản ánh được sự phân chia thông tin so với ngưỡng bình quân, với hiệp phương sai sẽ phản ánh sự liên kết tuyến tính giữa 2 biến.
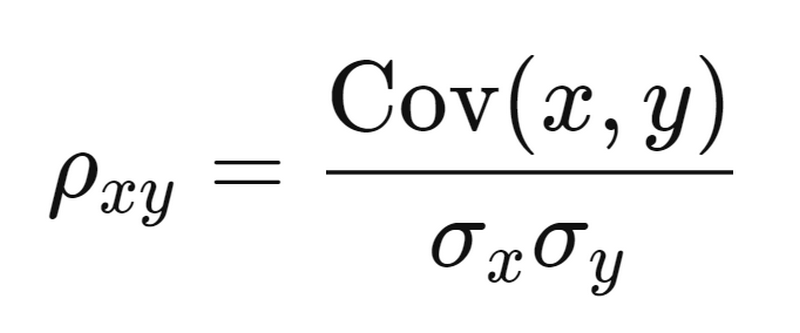
3. Ứng dụng của hệ số tương quan (Correlation Coefficient) trong tài chính
Hệ số tương quan có giá trị được phản ánh qua độ mạnh của những mối liên kết, chi tiết thì kết quả 0,2 phản ánh được sự liên kết đồng biến tuy nhiên không đáng kể và yếu. Với hệ số này thì chúng sẽ thể hiện được ý nghĩa nhất khi có giá trị 0,8, nhưng hệ số tương quan cùng giá trị tuyệt đối 0,9 hay có thể cao hơn sẽ phản ánh sự liên kết chặt chẽ.
Một ví dụ về ứng dụng của hệ số này ở lĩnh vực tài chính là:
Một hệ số tương quan có khả năng tìm ra được nhằm đo lường sự liên kết giữa mức giá cổ phiếu và dầu thổ tại một doanh nghiệp chuyên sản xuất dầu. DO những doanh nghiệp về dầu mỏ hay sinh lời cao hơn nếu mức giá dầu tăng cao và cả hai biến ra kết quả lớn hơn 0.
Một yếu tố nữa đó là việc đo lường về sự liên kết giữa các biến còn hỗ trợ cho nhà đầu tư tìm ra được thời điểm mà sự liên kết giữa các biến có sự biến động. Một cổ phiếu tại ngân hàng hay có mối tương quan khá tích cực cùng lãi suất, do mức lãi cho vay đa phần dựa vào lãi suất thị trường:
Khi mà giá cổ phiếu của ngân hàng giảm mà lãi suất tăng thì khi đó sẽ có khá nhiều nghi vấn được đặt ra.
Khi mà giá cổ phiếu ngân hàng tăng mà lãi suất tăng thì có thể nói rằng 2 biến này đang có mối tương quan dương.