Chắc rằng mọi người đã khá là quen thuộc đối với thuật ngữ dãy Fibonacci trong C là gì rồi. Trong bài viết hôm nay, chúng tôi sẽ trình bày chi tiết định nghĩa về chúng cũng như cách thức để có thể in dãy số này một cách cụ thể. Bạn đọc hãy theo dõi để nắm mọi thông tin liên quan nhé. Xem ngay!
Định nghĩa dãy Fibonacci trong C là gì?
Dãy Fibonacci trong C là gì? Chúng là một dãy số vô hạn bao gồm những số tự nhiên được bắt đầu bởi hai phần tử là 0 hay 1 với 1. Những phần tử này được cài đặt và thiết lập theo những quy tắc đó là mỗi phần tử luôn bằng với tổng số của hai phần tử trước chúng.
Lịch sử của dãy Fibonacci trong C như thế nào?
Dãy Fibonacci trong C được một nhà toán học đến từ Ý tên là Fibonacci phát minh ra, ông công bố nó vào thời điểm 1202 tại quyển sách Liber Abacci. Đây là quyển sách nói về toán đồ dựa theo hai bài toán cụ thể, đó là bài toán con thỏ cùng với bài toán số các “cụ tổ” đối với một con ong đực. Bên cạnh đó, một nhà văn đồng thời cũng là nhà toán học của nước Anh tên là Henry Dudeney cũng đã nghiên cứu trên bò sữa và đưa ra những kết quả gần giống như vậy.
Vào thế kỷ XIX, một nhà toán học với tên gọi là Edouard Lucas đã xuất bản ra một bộ sách bao gồm bốn tập với chủ đề về toán học giải trí. Tại đây, ông đã sử dụng tên Fibonacci dùng để gọi tên những dãy số cho kết quả từ bài toán của quyển Liber Abaci, một bài toán đã tạo nên dỹ Fibonacci.
Các bài toán mở đầu nên dãy Fibonacci trong C là gì?
Sau đây là hai bài toán đã được trích xuất từ quyển sách Liber Abacci bởi tác giả Fibonacci viết vào thời điểm năm 1202. Đây là các bài toán mẫu mực đem lại sự khảo sát cho dãy Fibonacci trong. Chi tiết như là:
Bài toán số con thỏ
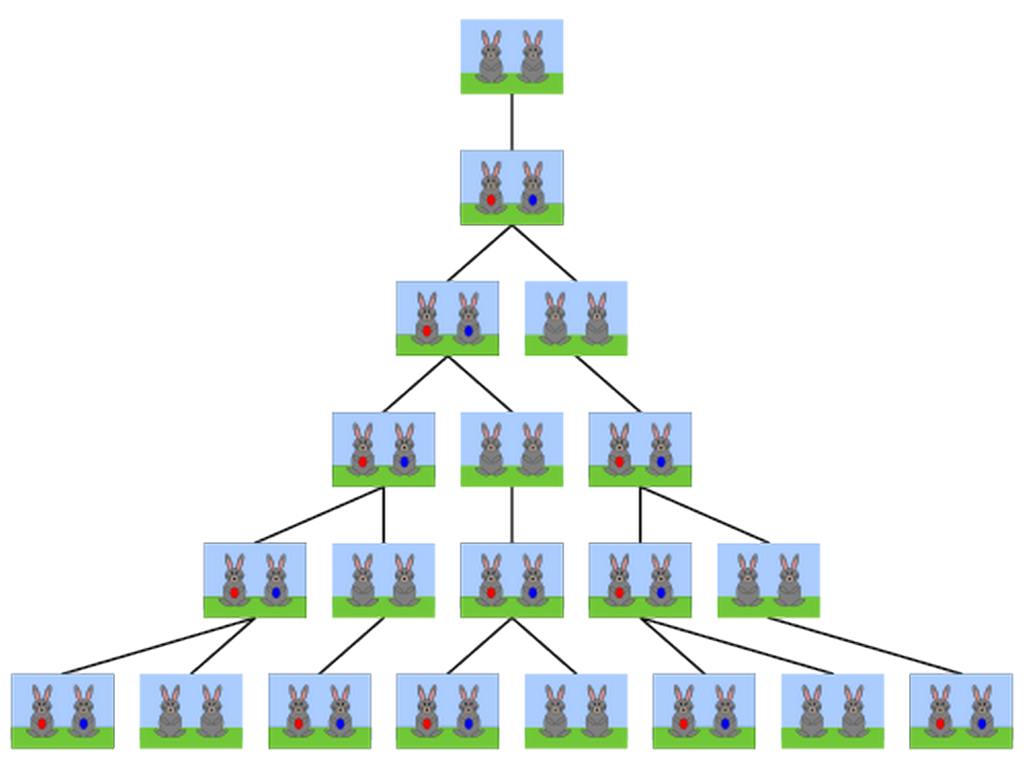
Một cặp thỏ bao gồm một con thỏ cái cùng với một con thỏ đực không sinh cho đến khi chúng vừa đạt hai tháng tuổi. Tức là sau khi vừa đủ tuổi là 2 tháng, đối với mỗi cặp thỏ sẽ sinh ra một cặp thỏ con, cũng bao gồm một con thỏ cái và mỗi con thỏ đực trong từng tháng. Vậy hỏi sau n tháng thì sẽ có bao nhiêu cặp thỏ, nếu như vào đầu tháng Giêng (đầu năm) có một cặp thỏ mới ra đời.
Với hình vẽ ở trên, chúng ta có thể quy ước như sau:
- Đôi thỏ màu xám chính là đôi thỏ có độ tuổi 1 tháng tuổi.
- Đôi thỏ đã được đánh dấu bởi màu xanh và màu đỏ sẽ là đôi thỏ có chức năng sinh sản.
Dựa vào đó chúng ta có thể nhận thấy:
- Vào tháng Giêng với tháng Hai thì sẽ chỉ có duy nhất một cặp thỏ
- Vào tháng Ba thì cặp thỏ trên sẽ sinh sản ra một cặp thỏ con, từ đó tại tháng này sẽ có hai cặp thỏ.
- Vào tháng Tư thì sẽ chỉ có cặp thỏ đầu tiên sinh con, do đó vào thời điểm này chỉ có 3 cặp thỏ mà thôi.
- Vào tháng Năm thì có đến hai đôi thỏ bao gồm cặp thỏ ban đầu cùng với cặp thỏ vừa được sinh ra vào tháng Ba phía trên cùng đẻ con, nên tại tháng này sẽ có 5 cặp thỏ (2 cặp + 3 cặp).
- Vào tháng Sáu, lúc này sẽ có ba cặp thỏ, bao gồm 2 cặp thỏ ban đầu cùng với cặp thỏ đã được đẻ ra vào thời điểm tháng Tư cùng đẻ còn. Do đó lúc này sẽ có 8 cặp thỏ ( 3 cặp + 5 cặp).
Tổng chung, nếu như n là một số tự nhiên khác 0, chúng ta gọi f(n) là số cặp thỏ đã có vào các tháng thứ n. Lúc này ta được:
- Với n bằng 1 chúng ta sẽ có f(1) bằng 1
- Với n bằng 2 chúng ta sẽ có f(2) bằng 1
- Với n bằng 3 chúng ta sẽ có f(3) bằng 2
Vì vậy với n lớn hơn 2 thì chúng ra sẽ có f(n) bằng f(n-1) cộng f(n-2).
Việc này có thể được giải thích một cách đầy đủ như sau: Các cặp thỏ được tạo ra ở tháng n-1 sẽ không thể đẻ con vào tháng thứ n. Và vào tháng này cặp thỏ ở tháng thứ n-2 sẽ tạo ra một cặp thỏ con, vì vậy số cặp thỏ được tạo ra vào tháng thứ n là mức giá trị của f(n-2).
Số các “cụ tổ” của một con ong đực
Đây là bài toán về dãy Fibonacci trong C thứ hai. Tác giả đã mô tả dãy số này bởi những tổ tiên của một con ong đực cụ thể như sau: Loài ong sẽ có thể tiến hành thụ tinh đơn tính hay là lưỡng tính. Ví dụ:
- Nếu như một trứng ong được thụ tinh từ chính con ong cái nó nở nên một con ong đực.
- Mặc dù vậy, nếu như một trứng được thụ tinh từ một con ong đực, nó sẽ trở thành một con ong cái.
- Do đó, một con ong đực lúc này sẽ có một con ong mẹ và một con ong cái sẽ có cả mẹ lẫn bố.
Bắt đầu chúng ta tính toán những con ong tổ tiên đối với một con ong đực. Xét về một con ong đực vào thế hệ thứ n, chúng ta sẽ nhìn thấy như sau:
- Trước khoảng một đời, vào thế hệ thứ n-1 thì một con ong đực sẽ chỉ có duy nhất một con ong cái là mẹ.
- Vào trước khoảng hai đời tức là thế hệ thứ n-2 thì một con ong cái vào đời thứ n-1 sẽ có hai bố mẹ, với một con ong bố (hay ong đực) cùng với một con ong cái (hay ong mẹ). Hai con ong sẽ bao gồm một cái một đực.
- Trước khoảng ba đời, nghĩa là thế hệ thứ n-3: một con ong cái ở thế hệ thứ n-2 sẽ có hai bố mẹ, trong đó một ong đực (bố) cùng với một ong cái (mẹ), ngoài ra một con ong đực vào thế hệ n-2 sẽ có một con ong mẹ ( 3 con ong bao gồm hai con ong cái và một con ong đực)
- Trước khoảng bốn đời, tại thế hệ n-4 thì đối với hai con ong cái thì mỗi con lúc này sẽ có hai bố hai mẹ. Đồng thời với mỗi con ong đực sẽ có một ong mẹ ( 5 con ong sẽ bao gồm 3 con ong cái và 2 con ong đực).
Tiếp tục quá trình trên thì chúng ta thu được dãy Fibonacci. Do đó, quá trình giải quyết của hai bài toán này của Fibonacci đem lại việc khảo sát dãy số dạng f(n) được xác định như sau: f(0) bằng 0; f(1) bằng 1; f(2) bằng 1; f(n) bằng f(n-1) cộng f(n-2) với mức n>2.
Dãy Fibonacci trong C đối với tự nhiên
Người ta đã chứng minh được với công thức tổng quát của dãy số này cụ thể. Dãy Fibonacci trong C này đã xuất hiện ở mọi nơi trong tự nhiên. Những chiếc lá của những cành cây mọc riêng biệt, tạo nên các khoảng tương ứng cùng với dãy số này.
Các số ở trong dãy số này xuất hiện kể cả ở trong các bông hoa. Đa số những bông hoa có số canh hoa sẽ là một trong những số bao gồm như 3, 5, 8, 13, 21, 34, 55 hay là 80. Đối với hoa loa kèn có ba cánh, các hoa họ Mao Lương sẽ có năm cánh, hay hoa phi yến thông thường năm cánh, hoa cúc tây sẽ có 21 cánh, hoa cúc vạn thọ thì có khoảng 13 cánh,…

Nếu như mọi người quan sát kỹ những “mắt” tại vỏ của những quả thơm chín, chúng ta đều dễ dàng thấu được những mắt tại hai đường vòng cung chéo tại vỏ quả quả dứa là hai dãy số của Fibonacci, ví dụ như 13 hoặc là 21.
Vừa rồi là một số chia sẻ chúng tôi muốn gửi đến bạn đọc về chủ đề dãy Fibonacci trong C. Mong rằng sẽ hữu ích và được bạn đọc áp dụng thành công trong cuộc sống!